红黑树学习笔记-新增节点
概述
利用过年放假的空闲时间,把红黑树又复习了一遍,在复习的过程中又有了一些新的收获,红黑树暴露给外部有查询、 增加、删除功能接口,同时提供了一个非功能性功能,保证所有的查询、增加、删除操作都在O(lgN)的时间内返回结果。这个非功能性特性就是依靠红黑树内部的动态平衡的机制来保持的。我们做系统开发,产品设计的时候,或者设计一个时间阶段的人生目标,都可以参考红黑树的动态平衡思想。本文会解释红黑树的一些特性和新增加节点的时候,它内部维持动态平衡的过程, 然后再另一篇文章里介绍如何在删除节点的时候维持动态平衡,最后会有一篇文章,是基于红黑树的发散思考,我们如何将红黑树的动态平衡思想应用到技术以外的世界里。
红黑树解释
红黑树的标准
-
每个节点必须是红色或者黑色
-
根节点必须是黑色
-
每个路径不能同时包含连续两个红色节点
-
每个从根节点到叶子节点的路径上必须包含相同数量的黑色节点
-
每个叶子节点的子节点都为空,为默认为黑色节点
-
每次插入的新节点都为红色
特性4保证红黑树不会存在最短路径和最长路径相差两倍的情况。 每次插入新的节点不会破坏特性1、4、5,6但是会破坏特性2,3, 那么我们就要思考分别在什么场景下会破坏特性2、3,下面就开始分别介绍有哪些场景会破坏特性2和3。
Case 1 父节点为空
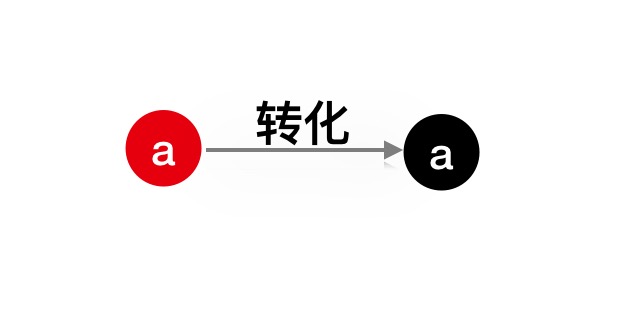
红黑树为空的时候,如果我们插入一个新节点,根据性质6,所以该节点的颜色为红色。因为只有一个节点,所以该节点为根节点, 但是由于性质2,所以我们需要调整该节点的颜色从红色改为黑色,如下图所示:
Case 2 新节点的父节点不为空,并且叔叔节点为黑色,如下图所示
在这个场景下,红黑树的性质全部都满足,因此我们不需要做任何调整。
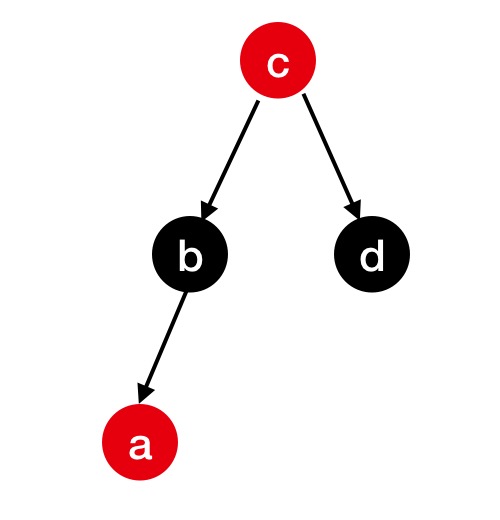
Case 3 父节点不为空并且叔叔节点、父节点都为红色,如下图所示
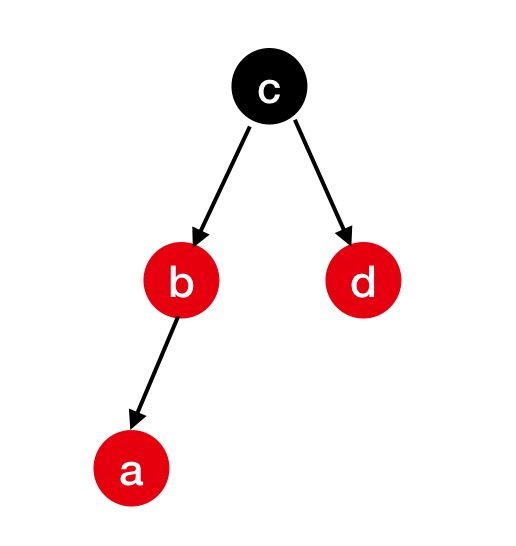
在这个场景下,由于破坏了性质3,所以我们需要调整父节点、叔叔节点和祖父节点的颜色,修复的结果如下:
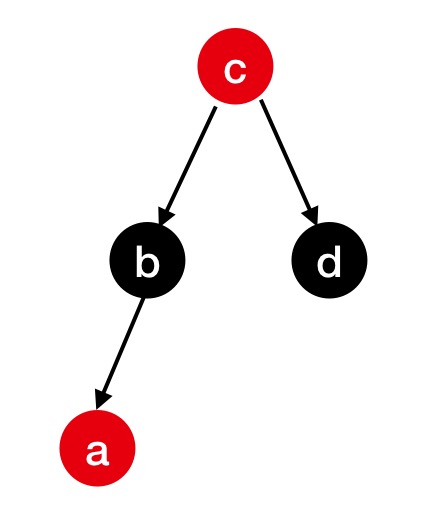
因为a的父节点和叔父节点都变为黑色,所以父亲节点路径和叔父节点路径下的黑色节点的数量保持不变。所以不会破坏性质4。 由于祖父节点从黑色变为了红色,就有可能破坏性质2和性质3,因此我们需要将祖父节点当成新节点,再从 case 1 再依次处理。
case 4 父节点不为空且为红色,新插入节点为父节点的右节点,父亲节点为祖父节点的右节点,或者相反的场景,具体如下图:

新插入的节点b或者d,需要分别向左旋转或者向右选择,b节点向左旋转后,a节点和b节点会交换位置,d节点向右旋转,e和d节点会交换位置,但都破坏了性质3,所以我们还需要继续调整,此时旋转后的场景就是case 5的情况了。
case 5 如果新插入的节点为父节点的右节点,父节点为红色,且叔父节点为空
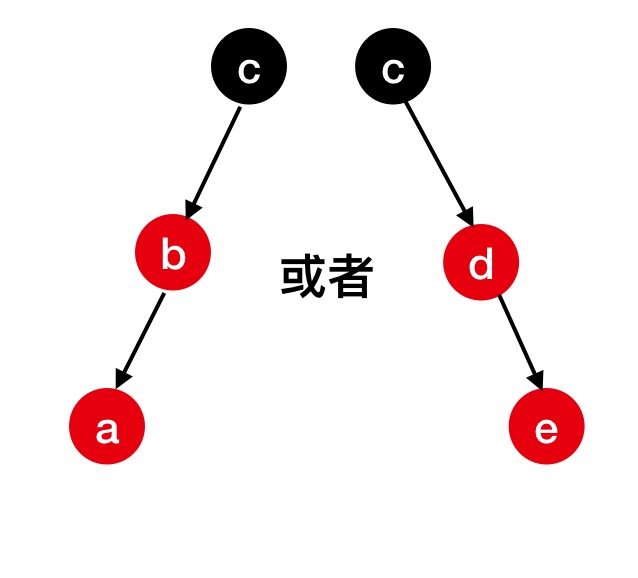
此时我们需要向右旋转a节点的祖父节点和向左旋转e的祖父节点,然后基于a节点和e节点重置颜色,如下图:
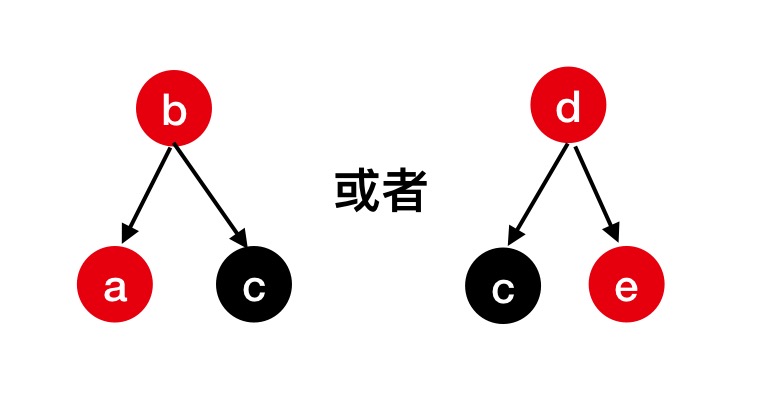
再基于a节点或者e节点重置颜色,如下图:
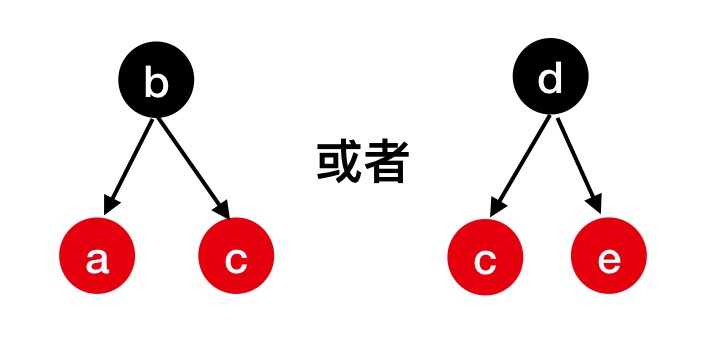
因为经过右旋和重置颜色后,左右路经上的黑色节点数量保持不变,因此不再需要调整。
总结
在插入节点的时候,经过如上步骤,我们可以维持红黑树的5个性质。下面会继续介绍如何在删除节点时维持这5个性质。